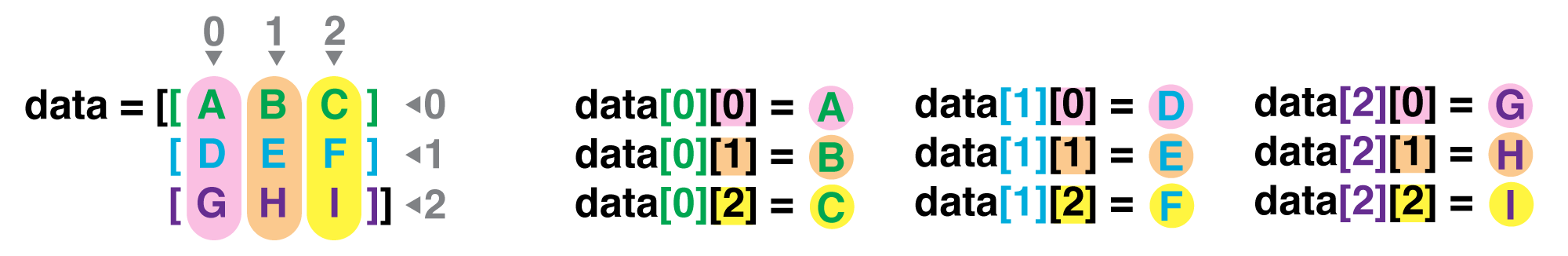Reading in Tabular Data
Overview
Teaching: 20 min
Exercises: 30 minQuestions
How can I load tabular data files in Python?
Objectives
Read tabular data from a file into a program.
Select individual values and subsections from data.
Perform operations on arrays of data.
In this lesson we will take what we’ve learnt about Python and start applying it to our arthritis inflammation data by loading some data in and performing the first bits of analysis.
For this part, we would recommend switching back to IPython while you’re still exploring the datasets as it will print out the large tables of data in a sensible way!
Loading data into Python
In order to load our inflammation data, we are going to use a library called NumPy. This module contains many numerical routines for data analysis and we will only be scratching the surface of what it can do in this course — it is well worth having a look to see what else is there!
Load in the data
The arthritis data is recorded in comma-separated list files To load this, use the function
loadtxtprovided bynumpyusing thefnameargument for the filenameinflammation-01.csvanddelimiterargument set as,. Assign this to a variable and theSolution
import numpy data = numpy.loadtxt(fname='inflammation-01.csv', delimiter=',') print(data)
You should hopefully have found the output looking like this:
array([[ 0., 0., 1., ..., 3., 0., 0.],
[ 0., 1., 2., ..., 1., 0., 1.],
[ 0., 1., 1., ..., 2., 1., 1.],
...,
[ 0., 1., 1., ..., 1., 1., 1.],
[ 0., 0., 0., ..., 0., 2., 0.],
[ 0., 0., 1., ..., 1., 1., 0.]])
The loadtxt function has loaded all the data from the inflammation-01.csv file and stored it
in an object. By default,
only a few rows and columns are shown
(with ... to omit elements when displaying big arrays).
To save space,
Python displays numbers as 1. instead of 1.0
when there’s nothing interesting after the decimal point.
This object looks a bit like a list of lists (note the square brackets!) but let’s check
exactly what it is by using the type function:
print(type(data))
<class 'numpy.ndarray'>
The output tells us that data currently refers to
an N-dimensional array, the functionality for which is provided by the NumPy library.
These arrays are similar to lists but you can do a lot more with them and they are
used throughout the numpy library.
These data correspond to arthritis patients’ inflammation.
The rows are the individual patients, and the columns
are their daily inflammation measurements.
Data Type and Shape
When we created the variable
datato store our arthritis data, we didn’t just create the array; we also created information about the array, called members or attributes. These members are accessed just like functions on an object or from a module using the.operator.Use the
dtypeandshapemembers of yourdatavariable to find out what the array contains and how many rows and columns it has.Solution
print(data.dtype) print(data.shape)
This should have told you that the array contains float64 or floating point numbers and
has 60 rows and 40 columns.
If we want to get a single number from the array, we must provide an index in square brackets after the variable name, just as we do in math when referring to an element of a matrix and how we accessed elements in strings and lists. However, our inflammation data has two dimensions, so we will need to use two indices to refer to one specific value. Here is where NumPy arrays differ significantly from normal lists in that you can give both indices in the square brackets:
print('first value in data:', data[0, 0])
first value in data: 0.0
print('middle value in data:', data[30, 20])
middle value in data: 13.0
The expression data[30, 20] accesses the element at row 30, column 20. As with lists, NumPy arrays
are zero-indexed and so start from (0,0).
In the Corner
What may also surprise you is that when Python displays an array, it shows the element with index
[0, 0]in the upper left corner rather than the lower left. This is consistent with the way mathematicians draw matrices but different from the Cartesian coordinates. The indices are (row, column) instead of (column, row) for the same reason, which can be confusing when plotting data.
Arrays also know how to perform common mathematical operations on their values. The simplest operations with data are arithmetic: addition, subtraction, multiplication, and division. When you do such operations on arrays, the operation is done element-by-element. Thus:
doubledata = data * 2.0
will create a new array doubledata
each elements of which is twice the value of the corresponding element in data:
print('original:')
print(data[:3, 36:])
print('doubledata:')
print(doubledata[:3, 36:])
original:
[[ 2. 3. 0. 0.]
[ 1. 1. 0. 1.]
[ 2. 2. 1. 1.]]
doubledata:
[[ 4. 6. 0. 0.]
[ 2. 2. 0. 2.]
[ 4. 4. 2. 2.]]
If, instead of taking an array and doing arithmetic with a single value (as above), you did the arithmetic operation with another array of the same shape, the operation will be done on corresponding elements of the two arrays. Thus:
tripledata = doubledata + data
will give you an array where tripledata[0,0] will equal doubledata[0,0] plus data[0,0],
and so on for all other elements of the arrays.
print('tripledata:')
print(tripledata[:3, 36:])
tripledata:
[[ 6. 9. 0. 0.]
[ 3. 3. 0. 3.]
[ 6. 6. 3. 3.]]
Often, we want to do more than add, subtract, multiply, and divide array elements. NumPy knows how
to do more complex operations, too. If we want to find the average inflammation for all patients on
all days, for example, we can ask NumPy to compute data’s mean value:
print(numpy.mean(data))
6.14875
mean is a function that takes
an array as an argument.
Mean Value for a subset of data
Can you use what you know about slicing to calculate the mean value for a single patient (row) and column (day)?
Solution
# Single patient mean print(numpy.mean(data[0,:])) # Single day mean print(numpy.mean(data[:,0]))
NumPy has lots of useful functions that take an array as input. Let’s use three of those functions to get some descriptive values about the dataset. We’ll also use multiple assignment, a convenient Python feature that will enable us to do this all in one line.
maxval, minval, stdval = numpy.max(data), numpy.min(data), numpy.std(data)
print('maximum inflammation:', maxval)
print('minimum inflammation:', minval)
print('standard deviation:', stdval)
Here we’ve assigned the return value from numpy.max(data) to the variable maxval, the value
from numpy.min(data) to minval, and so on.
maximum inflammation: 20.0
minimum inflammation: 0.0
standard deviation: 4.61383319712
Sorting Out References
What does the following program print out?
first, second = 'Grace', 'Hopper' third, fourth = second, first print(third, fourth)Solution
Hopper Grace
When analyzing data, though, we often want to look at variations in statistical values, such as the maximum inflammation per patient (as in the next diagram on the left) or the average inflammation per day (as in the diagram on the right). As the diagram below shows, we want to perform the operation across an axis:
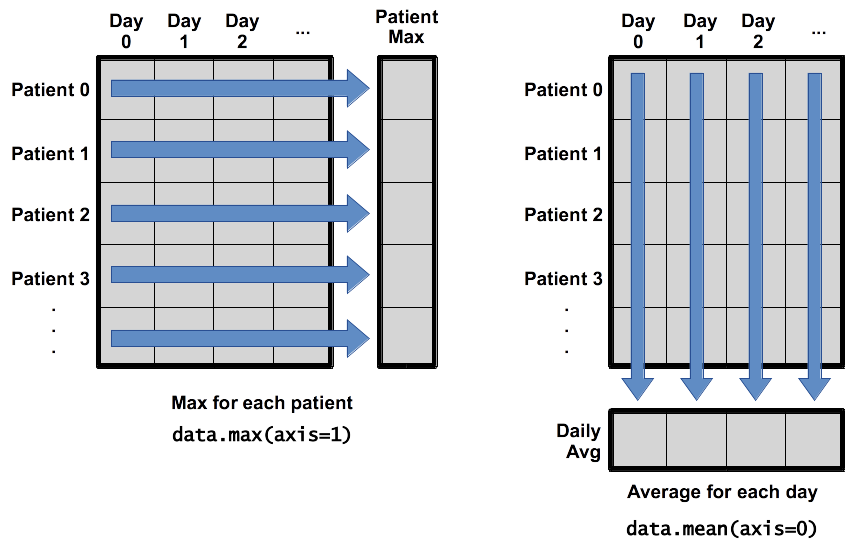
To support this functionality, most array functions allow us to specify the axis we want to work on. If we ask for the average across axis 0 (rows in our 2D example), we get:
print(numpy.mean(data, axis=0))
[ 0. 0.45 1.11666667 1.75 2.43333333 3.15
3.8 3.88333333 5.23333333 5.51666667 5.95 5.9
8.35 7.73333333 8.36666667 9.5 9.58333333
10.63333333 11.56666667 12.35 13.25 11.96666667
11.03333333 10.16666667 10. 8.66666667 9.15 7.25
7.33333333 6.58333333 6.06666667 5.95 5.11666667 3.6
3.3 3.56666667 2.48333333 1.5 1.13333333
0.56666667]
As a quick check, we can ask this array what its shape is:
print(numpy.mean(data, axis=0).shape)
(40,)
The expression (40,) tells us we have an N×1 vector,
So each entry is the average inflammation over all patients for that day
and there is a single entry per day.
If we average across axis 1 (columns in our 2D example), we get:
print(numpy.mean(data, axis=1))
[ 5.45 5.425 6.1 5.9 5.55 6.225 5.975 6.65 6.625 6.525
6.775 5.8 6.225 5.75 5.225 6.3 6.55 5.7 5.85 6.55
5.775 5.825 6.175 6.1 5.8 6.425 6.05 6.025 6.175 6.55
6.175 6.35 6.725 6.125 7.075 5.725 5.925 6.15 6.075 5.75
5.975 5.725 6.3 5.9 6.75 5.925 7.225 6.15 5.95 6.275 5.7
6.1 6.825 5.975 6.725 5.7 6.25 6.4 7.05 5.9 ]
which is the average inflammation per patient across all days.
Stacking Arrays
Arrays can be concatenated and stacked on top of one another, using NumPy’s
vstackandhstackfunctions for vertical and horizontal stacking, respectively.import numpy A = numpy.array([[1,2,3], [4,5,6], [7, 8, 9]]) print('A = ') print(A) B = numpy.hstack([A, A]) print('B = ') print(B) C = numpy.vstack([A, A]) print('C = ') print(C)A = [[1 2 3] [4 5 6] [7 8 9]] B = [[1 2 3 1 2 3] [4 5 6 4 5 6] [7 8 9 7 8 9]] C = [[1 2 3] [4 5 6] [7 8 9] [1 2 3] [4 5 6] [7 8 9]]
Change In Inflammation
This patient data is longitudinal in the sense that each row represents a series of observations relating to one individual. This means that the change in inflammation over time is a meaningful concept.
The
numpy.diff()function takes a NumPy array and returns the differences between two successive values along a specified axis. For example, a NumPy array that looks like this:npdiff = numpy.array([ 0, 2, 5, 9, 14])Calling
numpy.diff(npdiff)would do the following calculations and put the answers in another array.[ 2 - 0, 5 - 2, 9 - 5, 14 - 9 ]numpy.diff(npdiff)array([2, 3, 4, 5])Which axis would it make sense to use this function along? How would you create an array of these changes?
Solution
Since the rows (axis 0) are patients, it does not make sense to get the difference between two arbitrary patients. The columns (axis 1) are in days, so the difference is the change in inflammation – a meaningful concept.
numpy.diff(data, axis=1)If the shape of an individual data file is
(60, 40)(60 rows and 40 columns), what would the shape of the array be after you run thediff()function and why?Solution
The shape will be
(60, 39)because there is one fewer difference between columns than there are columns in the data.How would you find the largest change in inflammation for each patient? Does it matter if the change in inflammation is an increase or a decrease? Hint: Try to combine the
numpy.max(),numpy.diff()andnumpy.absolute()functions.Solution
By using the
numpy.max()function after you apply thenumpy.diff()function, you will get the largest difference between days.numpy.max(numpy.diff(data, axis=1), axis=1)array([ 7., 12., 11., 10., 11., 13., 10., 8., 10., 10., 7., 7., 13., 7., 10., 10., 8., 10., 9., 10., 13., 7., 12., 9., 12., 11., 10., 10., 7., 10., 11., 10., 8., 11., 12., 10., 9., 10., 13., 10., 7., 7., 10., 13., 12., 8., 8., 10., 10., 9., 8., 13., 10., 7., 10., 8., 12., 10., 7., 12.])If inflammation values decrease along an axis, then the difference from one element to the next will be negative. If you are interested in the magnitude of the change and not the direction, the
numpy.absolute()function will provide that.Notice the difference if you get the largest absolute difference between readings.
numpy.max(numpy.absolute(numpy.diff(data, axis=1)), axis=1)array([ 12., 14., 11., 13., 11., 13., 10., 12., 10., 10., 10., 12., 13., 10., 11., 10., 12., 13., 9., 10., 13., 9., 12., 9., 12., 11., 10., 13., 9., 13., 11., 11., 8., 11., 12., 13., 9., 10., 13., 11., 11., 13., 11., 13., 13., 10., 9., 10., 10., 9., 9., 13., 10., 9., 10., 11., 13., 10., 10., 12.])
Key Points
Use the
numpylibrary to work with arrays in Python.The expression
array.shapegives the shape of an array.Use
array[x, y]to select a single element from a 2D array.All the indexing and slicing that works on strings and lists also works on arrays.
Use
numpy.mean(array),numpy.max(array), andnumpy.min(array)to calculate simple statistics.Use
numpy.mean(array, axis=0)ornumpy.mean(array, axis=1)to calculate statistics across the specified axis.